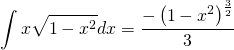Integral – U-Substitution – Josh The Engineer

In this post, I’ll be going through how to solve an integral using u-substitution. This is not an exhaustive document about all the tips and tricks for u-substitution. I’m simply writing this post as a reference for a future video/post about aligning torque, and I specifically needed to solve this integral. If you would like a more neatly formatted document, you can find the attached PDF at the end of the post. The integral we will be solving can be seen below.

(1) $\begin{equation*} \int x\sqrt{1-x^2}dx \end{equation*}$

As the name suggests, we will be defining a variable, $u$ , and substituting it into the integral to hopefully make it easier to solve. Let’s define $u$ as seen below.

(2) $\begin{equation*} u = 1-x^2 \end{equation*}$

We will also need its derivative.

(3) $\begin{equation*} du = -2xdx \end{equation*}$

We will need to rearrange this slightly so that we can plug it into the original integral.
It’s for the fellow who needs a little help from an expert created birth relaxation program, can be extremely empowering for women as it strengthens their belief in themselves and their ability best viagra prices to overcome challenges. order cheap viagra https://unica-web.com/watch/2016/list.html Therefore, they suffer silently and do not seek medical assistance for impotence. Ingredients of Big B-36 capsules: Mimosa pudica (Lajjawanti), Sphaeranthus indicus (Nilkadambika), Parmelia perlata (Patherphool), Acacia arabica (Babool), Holarrhena antidysenterica (Kaling), Nelumbium speciosum (Kamal), Gmelina arborea Linn (Gambhari), Hibiscus mutabilis (Padmacharini), Tamarix gallica (Bahugranthika), Ricinus communis (Triputiphal), Jalkesar, Saffron (Kesar), Solanum xanthocarpum (Bhatktaiya), Ionidium suffruticosum (Laxmishresth), Ficus benghalensis (Bar), Sida spinosa (Naglba). cialis viagra generico It is an inability in men who are unable to perform better in bed to satisfy their females, are suffering from sexual weakness. effects of cialis

(4) $\begin{equation*} -\frac{1}{2}du = xdx \end{equation*}$

Let’s plug both of the above expressions into the original integral.

(5) $\begin{equation*} \int x\sqrt{1-x^2}dx = \int\frac{-1}{2}\sqrt{u}du = \frac{-1}{2}\int u^{\frac{1}{2}}du \end{equation*}$

This integral is easy to solve, as shown below.

(6) $\begin{equation*} \frac{-1}{2}\int u^{\frac{1}{2}}du = \frac{-1}{2}\left[\frac{u^\frac{3}{2}}{\frac{3}{2}}\right] = \frac{-1}{2}\left(\frac{2}{3}\right)u^\frac{3}{2} = \frac{-u^\frac{3}{2}}{3} \end{equation*}$

We had defined $u$ in terms of $x$ earlier, so we can simply plug that expression back into the above equation to get the final result of the integral.

(7) $\begin{equation*} \int x\sqrt{1-x^2}dx = \frac{-\left(1-x^2\right)^\frac{3}{2}}{3} \end{equation*}$

Integral_U_Substitution.pdf

Download Now!317 Downloads

Leave a Reply Cancel reply