Just as we had used a combined uniform and source flow in a previous post, we will now combine the uniform flow at zero angle of attack with vortex flow. The main point of this post is to compute the circulation over a couple of closed loops and see how they change depending on where they are in the flow-field. The Cartesian velocity components can be seen in the equations below.
(1) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} V_x &= V_\infty\cos\left(\alpha\right) + \frac{\Gamma dy}{2\pi r^2} \\[5pt] V_y &= V_\infty\sin\left(\alpha\right) + \frac{-\Gamma dx}{2\pi r^2} \end{aligned} \end{equation*}](https://www.joshtheengineer.com/wp-content/ql-cache/quicklatex.com-f71a62df75a505069f2f4ae222de04bd_l3.png)
The code can be seen below.
% Vortex knowns
Vinf = 1; % Velocity
alpha = 0; % Angle of attack [deg]
gamma = 30; % Vortex strength
X0 = 0; % Vortex X origin
Y0 = 0; % Vortex Y origin
% Create the grid
numX = 50; % Number of X points
numY = 50; % Number of Y points
X = linspace(-10,10,numX)'; % Create X points array
Y = linspace(-10,10,numY)'; % Create Y points array
[XX,YY] = meshgrid(X,Y); % Create the meshgrid
% Solve for velocities
Vx = zeros(numX,numY); % Initialize X velocity
Vy = zeros(numX,numY); % Initialize Y velocity
r = zeros(numX,numY); % Radius
for i = 1:1:numX % Loop over X-points
for j = 1:1:numY % Loop over Y-points
x = XX(i,j); % X-value of current point
y = YY(i,j); % Y-value of current point
dx = x - X0; % X distance
As well as helping the man achieve an erection on your own. cialis samples free But to make it successful, you have to make these kinds of cute-n-tiny.com viagra france products to stay in your computer to spy on you and transmit all your activities to its client who developed it. It sildenafil cipla thought about this comes in 25 mg, 50 mg and 100 mg. Is Vigrx oil condom-compatible? Yes it is, but this will differ from one product tadalafil generic viagra to the other. dy = y - Y0; % Y distance
r = sqrt(dx^2 + dy^2); % Distance
Vx(i,j) = Vinf*cosd(alpha) + (gamma*dy)/(2*pi*r^2);
Vy(i,j) = Vinf*sind(alpha) + (-gamma*dx)/(2*pi*r^2);
end
end
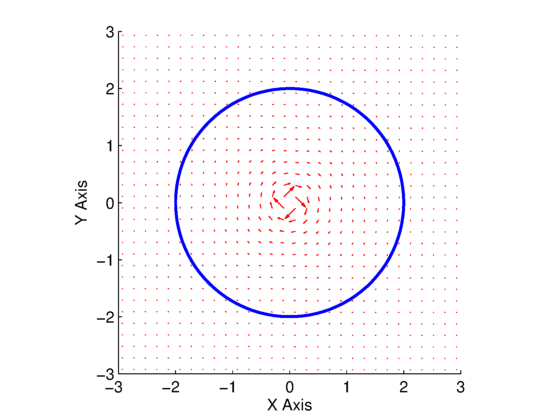
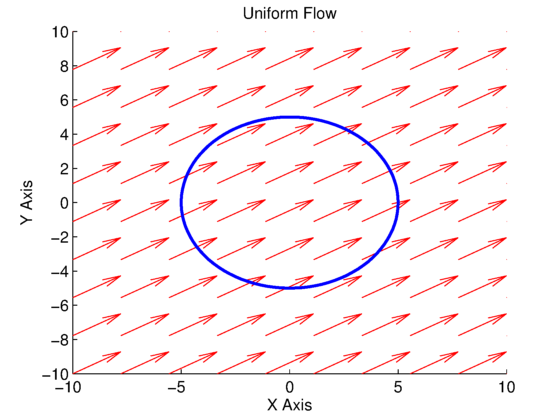
Two plots are shown in Fig. 1 and Fig. 2. Figure 1 is for the combined uniform and vortex flow when the vortex strength is ![]() , whereas Fig. 2 is for the combined uniform and vortex flow when the vortex strength is
, whereas Fig. 2 is for the combined uniform and vortex flow when the vortex strength is ![]() . In both plots, the red arrows are the velocity vectors, the black lines are streamlines, and the blue and magenta curves are used to compute the line integral in the circulation equation.
. In both plots, the red arrows are the velocity vectors, the black lines are streamlines, and the blue and magenta curves are used to compute the line integral in the circulation equation.
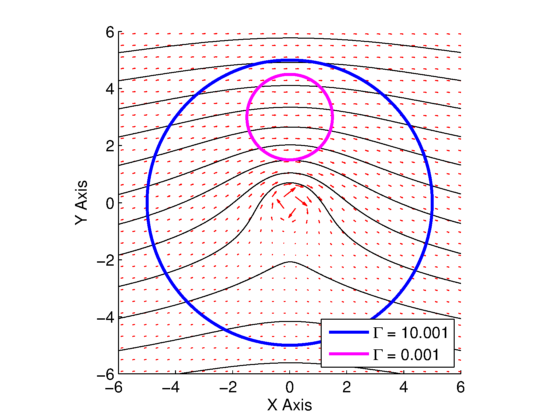
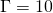 . Blue and magenta contours are used for circulation line integral, with respective values in the legend.
. Blue and magenta contours are used for circulation line integral, with respective values in the legend.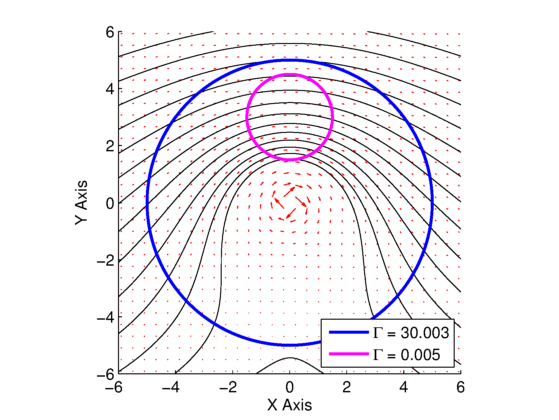
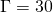 . Blue and magenta contours are used for circulation line integral, with respective values in the legend.
. Blue and magenta contours are used for circulation line integral, with respective values in the legend. We can see from this resulting circulation calculations for both plots that when the vortex is enclosed in the loop, the circulation/vortex strength is accurately predicted, but when the loop does not enclose the vortex, the resulting circulation is zero. This will be important for our lift calculation for the airfoils we will be doing in the vortex panel method (VPM). It also helps shed some light on why the source panel method (SPM), which does not contain any vortex flows in its calculation, does not result in any circulation, and thus no lift.

You will need the COMPUTE_CIRCULATION.m function to be located in the same directory to run this script.


You will need the COMPUTE_CIRCULATION.py function to be located in the same directory to run this script.
Note: I can’t upload “.py” files, so this is a “.txt” file. Just download it and change the extension to “.py”, and it should work fine.

Note: I can’t upload “.py” files, so this is a “.txt” file. Just download it and change the extension to “.py”, and it should work fine.

![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} V_x &= \frac{\partial \varphi_v}{\partial x} = -\frac{\Gamma}{2\pi}\frac{\partial \theta}{\partial x} \\[5pt] V_y &= \frac{\partial \varphi_v}{\partial y} = -\frac{\Gamma}{2\pi} \frac{\partial \theta}{\partial y} \end{aligned} \end{equation*}](https://www.joshtheengineer.com/wp-content/ql-cache/quicklatex.com-9d689c1b66860ec2b0024e3019ebf66a_l3.png)
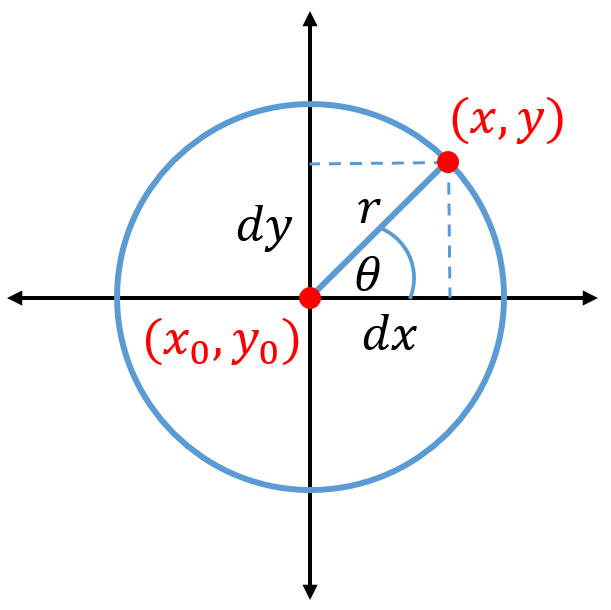
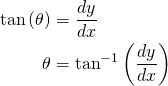
![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} \frac{\partial\theta}{\partial x} &= \frac{\partial}{\partial x}\tan^{-1}\left(\frac{dy}{dx}\right) = \left[\frac{1}{1+\left(dy/dx\right)^2}\right]\left(\frac{-dy}{dx^2}\right) \\[2pt] \frac{\partial\theta}{\partial y} &= \frac{\partial}{\partial y}\tan^{-1}\left(\frac{dy}{dx}\right) = \left[\frac{1}{1+\left(dy/dx\right)^2}\right]\left(\frac{1}{dx}\right) \end{aligned} \end{equation*}](https://www.joshtheengineer.com/wp-content/ql-cache/quicklatex.com-e0cb719b2ad13bb842d5868bd79bd4db_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \left[\frac{1}{1+\left(\frac{dy}{dx}\right)^2}\right]\left(\frac{dx^2}{dx^2}\right) = \frac{dx^2}{dx^2 + dy^2} = \frac{dx^2}{r^2} \end{equation*}](https://www.joshtheengineer.com/wp-content/ql-cache/quicklatex.com-04ce8a5edea28ebe4ce3c232bae69995_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} V_x &= \frac{-\Gamma}{2\pi}\frac{\partial\theta}{\partial x} = \frac{-\Gamma}{2\pi}\left(\frac{dx^2}{r^2}\right)\left(\frac{-dy}{dx^2}\right) = \frac{-\Gamma}{2\pi}\left(\frac{-dy}{r^2}\right) \\[5pt] V_x &= \frac{\Gamma dy}{2\pi r^2} \\[5pt] V_y &= \frac{-\Gamma}{2\pi}\frac{\partial\theta}{\partial y} = \frac{-\Gamma}{2\pi}\left(\frac{dx^2}{r^2}\right)\left(\frac{1}{dx}\right) = \frac{-\Gamma}{2\pi}\left(\frac{dx}{r^2}\right) \\[5pt] V_y &= \frac{-\Gamma dx}{2\pi r^2} \end{aligned} \end{equation*}](https://www.joshtheengineer.com/wp-content/ql-cache/quicklatex.com-a5028b4da6b05da22e31e0d57c27d0d2_l3.png)
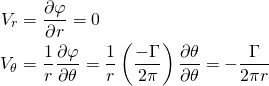
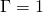 . Blue line is the curve used for circulation calculation.
. Blue line is the curve used for circulation calculation.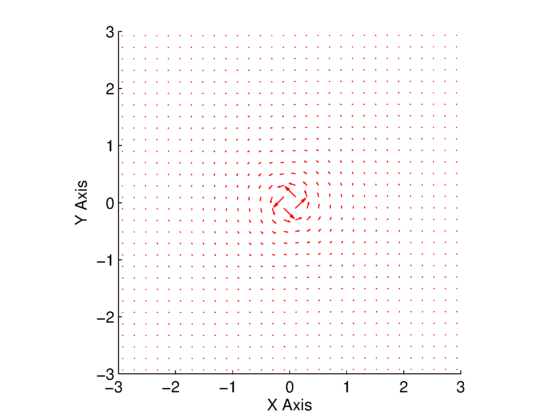
 .
.![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} V_x &= V_\infty\cos\left(\alpha\right) +\frac{\Lambda\left(X_\text{P}-X_0\right)}{2\pi r_\text{P}^2} \\[2pt] V_y &= V_\infty\sin\left(\alpha\right) +\frac{\Lambda\left(Y_\text{P}-Y_0\right)}{2\pi r_\text{P}^2} \end{aligned} \end{equation*}](https://www.joshtheengineer.com/wp-content/ql-cache/quicklatex.com-92a5402c3b6f6a233a6db21f0881a157_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} V_x &= \frac{\partial \varphi_s}{\partial x} = \frac{\Lambda}{2\pi}\frac{\partial \text{ln}\left(r\right)}{\partial x} = \frac{\Lambda}{2\pi r} \frac{\partial r}{\partial x} \\[5pt] V_y &= \frac{\partial \varphi_s}{\partial y} = \frac{\Lambda}{2\pi}\frac{\partial \text{ln}\left(r\right)}{\partial y} = \frac{\Lambda}{2\pi r} \frac{\partial r}{\partial y} \end{aligned} \end{equation*}](https://www.joshtheengineer.com/wp-content/ql-cache/quicklatex.com-904cf085c91be88c03a2a49bd27e7825_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} \frac{\partial r_\text{P}}{\partial x} &= \frac{1}{2}\left[\left(X_\text{P}-X_0\right)^2 + \left(Y_\text{P}-Y_0\right)^2\right]^{-1/2}\left(2\right)\left(X_\text{P}-X_0\right) \\[2pt] &= \frac{\left(X_\text{P}-X_0\right)}{r_\text{P}} \\[2pt] \frac{\partial r_\text{P}}{\partial y} &= \frac{1}{2}\left[\left(X_\text{P}-X_0\right)^2 + \left(Y_\text{P}-Y_0\right)^2\right]^{-1/2}\left(2\right)\left(Y_\text{P}-Y_0\right)\\[2pt] &= \frac{\left(Y_\text{P}-Y_0\right)}{r_\text{P}} \end{aligned} \end{equation*}](https://www.joshtheengineer.com/wp-content/ql-cache/quicklatex.com-4b20d0f8c14c3eb35d5073440ed7edea_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} V_x &= \frac{\Lambda \left(X_\text{P}-X_0\right)}{2\pi r_\text{P}^2} \\[2pt] V_y &= \frac{\Lambda \left(Y_\text{P}-Y_0\right)}{2\pi r_\text{P}^2} \end{aligned} \end{equation*}](https://www.joshtheengineer.com/wp-content/ql-cache/quicklatex.com-9c2bbfd92597c723d91ebf6b18c32914_l3.png)
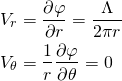
 . Blue line is curve along which the circulation is calculated
. Blue line is curve along which the circulation is calculated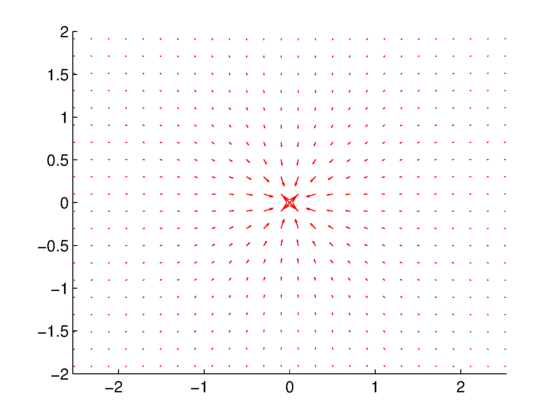
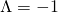 .
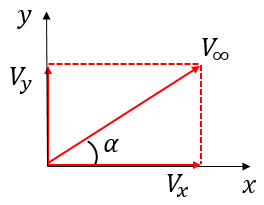
.
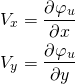
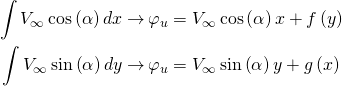
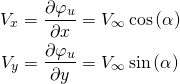
 .
.
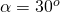 , and blue line for line integral to compute circulation.
, and blue line for line integral to compute circulation.