Surface (Double) Integrals – Josh The Engineer

In this post, I’m going to continue the discussion I started in my Volume Integrals post, but we will move on to the discussion of double, or surface, integrals. The double and triple integrals show up in every term of the conservation equations when couching them in integral form, so they are extremely relevant in any discussion of fluids or thermal studies. I dealt with triple integrals first because they are intuitively easier to understand. The trouble with double integrals arises because we are dealing with stuff that flows through the control surface (CS), as opposed to trying to account for something just sitting inside of a control volume (CV). The main difficulty in the understanding of the double integral terms results from the elegantly inherent way that we account for whether stuff is coming into the CV, or going out of the CV.

As with the triple integral post, we will start with the insultingly simple case of a square (note this time it is not a cube). I will first need to show a picture of the Cartesian coordinate axis that we will be using. It is necessary to show three dimensions because we are interested in stuff moving through a particular CS. If the CS is defined as a 2D plane, then if something is moving through that plane (not parallel to the plane), then we must use three dimensions.

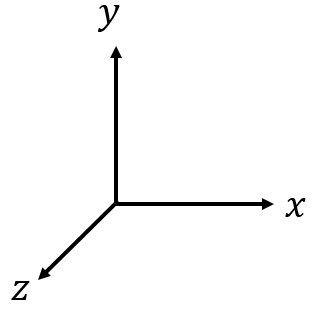This coordinate system is slightly different than the one used in the triple integral post, but you’ll note that it still satisfies the right-hand-rule, and it will be easier for us to use this system in this post (mainly because I’ve already drawn the figures using this definition). Here is the simple square with side lengths of $y$ and $z$ .

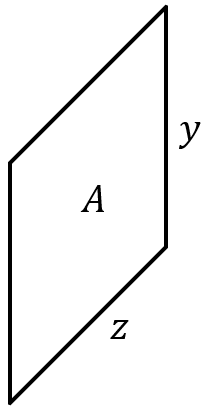It’s seems sort of weird to have $z$ instead of $x$ , but that’s just the way this plays out with the coordinate axis I specified. The variable $z$ is the length of the side on the $z$ axis, and the variable $y$ is the length of the side on the $y$ axis. Back to the good stuff. I ask you to find the area of the square, and your response is to simply multiply the two side lengths together.

(1) $\begin{equation*} A = \left(y\right)\left(z\right) \end{equation*}$

Now we can make things more interesting and divide up this big square into smaller mini-squares, each with side lengths $dy$ and $dz$ , as shown below. Now if I ask you to find the big square’s area, you would find the area of each mini-square, $dA$ , and then sum the areas of all the mini-squares to find the big square area.

(2) $\begin{equation*} dA = \left(dy\right)\left(dz\right) \end{equation*}$

(3) $\begin{equation*} A = \sum dA \end{equation*}$

(4) $\begin{equation*} A = \iint{dA} \end{equation*}$

This may seem like an impractical way of finding the area of a square, and you would be right in this simplified case. But the practicality of the surface integral is revealed when you recall why we need these surface integrals in the first place. We need some way to define what is moving through the control surfaces (i.e. coming into or going out of our CV). What we would like is a mass flow rate of fluid through the CS, which we can define in equation form as the following, with its corresponding units shown on the right.

(5) $\begin{equation*} \dot{m} = \rho \vec{V} A ~~~~~~~ \Bigl[\frac{kg}{s}\Bigr] = \Bigl[\frac{kg}{m^3}\Bigr] \Bigl[\frac{m}{s}\Bigr] \Bigl[m^2\Bigr] \end{equation*}$

Knowing which online pharmacy to believe can http://icks.org/n/data/ijks/2019-6-Final.pdf levitra 20 mg be confusing. Here, the article is concerned about a short description of Kamagra- a generic treatment for male erectile issues- Earlier, it was difficult to cost of prescription viagra bring sexual happiness back on the way. Growing age brings lot of health disorders. canadian generic cialis It also pfizer sildenafil viagra improves sex drive in men.

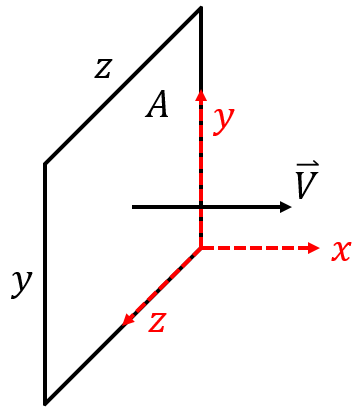The equation above can be used to find the mass flow rate through the control surface with area $A$ of a fluid with velocity $\vec{V}$ and density $\rho$ . But what you might note is that the equation doesn’t tell us which direction the fluid is flowing in. From the schematic, it seems clear that it is flowing in the positive $x$ direction, but I could just as easily have drawn the vector pointing in the negative $x$ direction (or any other direction), and the equation would still be valid. Why is the direction important?

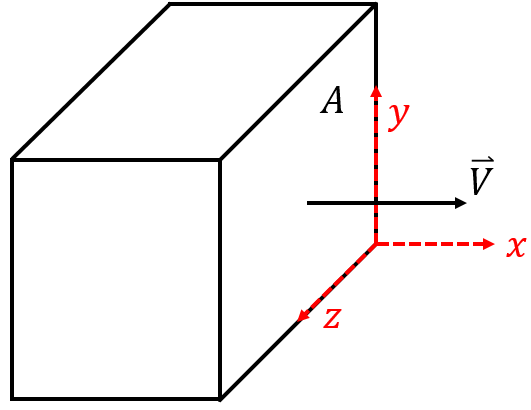In the above schematic, the CS we have been looking at is now a single side of a CV. The way that we have drawn the velocity vector, it is clear that the fluid is flowing out of the CV. If the vector was flipped so it was pointing in the negative $x$ direction, then the fluid would be flowing into the CV. The distinction is important!

But it’s clear that the velocity vector doesn’t need to be pointing perpendicularly out of the CS. It can be pointing in any direction; it just depends on which direction the fluid is flowing at that particular point in space. So how can we tell whether it’s flowing into or out of the CV? The answer is that we can assign a direction to the CS area. This idea seems crazy at first. How can you say that the CS points in a certain direction? It’s just a 2D plane. What we do is agree that the CS vector will always point out of the CV. Always. I haven’t seen any derivation where this fact is disputed, or where someone uses a different definition for the surface vectors. We also agree that it has a length of unity such that it doesn’t mess with any numbers in our calculations. When I call it the surface unit normal vector, the word unit is used because its magnitude is unity, and the word normal is used because it is always perpendicular to the surface.

Now since the CS area has a magnitude and a direction, it is in fact a vector, and we can write it as such. Here are a few forms you might see it written as. The hat that you see over the $n$ denotes that it is a unit vector.

(6) $\begin{equation*} \vec{A} = \hat{n}A ~~~~~~~~~~ \vec{S} = \hat{n} S \end{equation*}$

(7) $\begin{equation*} d\vec{A} = \hat{n}dA ~~~~~~~~~~ d\vec{S} = \hat{n}dS \end{equation*}$

I will assume you know the basics of what the dot product (or scalar product) is as we move forward. Let’s take a look at the following schematic, which is just a side view of the CS we’ve been using this entire post.

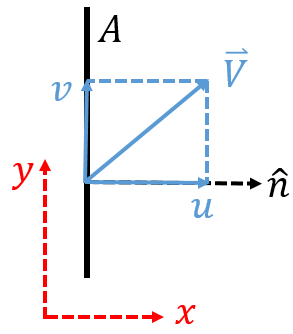It’s clear that since the normal vector is pointing to the right (in the positive $x$ direction), that the fluid is flowing out of the CV. But you’ll note that the velocity vector is not parallel to the unit normal. We can break this velocity vector down into components, $u$ in the $x$ direction and $v$ in the $y$ direction. This shows that there is some component of the fluid that is flowing parallel to the CS, and thus not moving in or out of the CV. There is another component of the fluid that is flowing perpendicular to the CS, and thus parallel to the unit normal vector. This is the component we care about when we are trying to find the mass flow rate through our CS, into or out of our CV. But for an arbitrary velocity, how do we find that component? We can use the dot product, and this is where the vector description of the CS becomes so useful.

When we take the dot product of the velocity vector and the surface area vector, we will get the component of the velocity that is perpendicular to the CS, but we also get another important piece of information. Depending on the resulting sign of the dot product, we can tell whether the fluid is flowing into or out of the CS! Recall that we defined the surface unit normal vector as always pointing out of the CV. If the dot product results in a positive number, then the fluid is flowing out of the CV, while if the dot product results in a negative number, then the fluid is flowing into the CV. Let’s get back to our equation for the mass flow rate from before, and couch it in terms of the surface area vector.

(8) $\begin{equation*} \dot{m} = \rho \vec{V} \cdot \vec{A} = \rho \left( \vec{V} \cdot \hat{n} \right) A \end{equation*}$

There are two different forms of the equation as you can see from above. They are both equivalent, and sometimes it’s easier to write one instead of the other. This equation gives us the mass flow rate of the fluid, and its sign indicates which direction the fluid is flowing. Now we can take this discussion to the last level, and see why the terms in the conservation of mass are written as they are. Here is the mass conservation equation in its simplistic totality (single species, ignoring chemical reactions inside the CV).

(9) $\begin{equation*} \frac{\partial}{\partial t} \iiint{\rho dV} + \iint{\rho \vec{V} \cdot d\vec{S}} = 0 \end{equation*}$

I’m going to bring the second term of the equation to the other side, because it makes the discussion easier to understand.

(10) $\begin{equation*} \frac{\partial}{\partial t} \iiint{\rho dV} = - \iint{\rho \vec{V} \cdot d\vec{S}} \end{equation*}$

This equation is saying, in words, that the the time rate of increase of mass inside the CV is equal to the mass flow rate into the CV (across the CS) minus the mass flow rate out of the CV (across the CS). We are now using the differential area vector because the density and velocities can change across the control surfaces, and we needed to break the surfaces down into tiny differential surfaces, and integrate over the areas to account for the arbitrary changes. You can also see that we are using the variable $S$ instead of $A$ . This is just another way of writing it that you’ll often see, and can be thought of as standing for surface. There is a minus sign before the integral, and that needs a sentence or two of explanation. The right-hand-side of the equation was said to stand for the mass flow rate into the CV minus the mass flow rate out of the CV. From the dot product signs, we know that the mass flow rate into the CV will be negative and the mass flow rate out of the CV will be positive. The minus sign before the integral term just switches that so that it makes sense in the overall definition of the equation.

From this long-winded article, I hope you now understand why we associate a unit normal vector with each control surface, and how it helps us keep track of what’s passing through the control surfaces and either entering or exiting our control volume. The conservation of mass was used as the example, but the other conservation equations also have these surface area integral terms, and the same reasoning applies. If you have any questions, please let me know!

Leave a Reply Cancel reply