Introduction to Incompressible Potential Flow

This post is not meant to be an exhaustive dive into potential flow; it is only meant as an introduction to incompressible potential flow and how we can use potential flow theory to get simplified solutions to some otherwise complicated problems.

When solving complex problems in aerodynamics, we can start with the most general equations we know, for instance, the Navier-Stokes equations (which themselves already have a couple of assumptions built in, but are not very limiting). These equations require detailed numerical solutions, so we would like to simplify them down by making some more valid assumptions. We will be making two assumptions here:

Irrotational flow (angular velocity/vorticity is zero)
Incompressible flow (density is constant)

The first assumption results in what we call potential flow theory, while the second assumption gives us the more specific incompressible potential flow, which we can use to calculate, for example, the flow around an airfoil.

Assumption: Irrotational

Let’s start with the assumption of irrotational flow. The vorticity is equal to the curl of the velocity ( $\nabla \times \vec{V}$ ), which we can derive in another post at a later date (or see Chapter 2.12 in Fundamentals of Aerodynamics by Anderson). For irrotational flow, this is equal to zero at every point in the flow. Physically, this means that the fluid elements have no angular velocity, and that they only translate through space (though you can have equal and opposite angular velocities of the fluid element’s connecting sides).

Since we now know for irrotational flow that $\nabla \times \vec{V} = 0$ , we need to find a form of $\vec{V}$ that always satisfies this equation. Note that $\vec{V} = 0$ satisfies the equation, but this is a trivial solution. Recall the vector identity that the curl of the gradient of a scalar is always equal to zero, $\nabla \times \left(\nabla \varphi\right) = 0$ . In this equation we are assuming that $\varphi$ is a scalar. Let’s run through the cross product calculation to see if this is true.

(1) $\begin{equation*} \nabla \times \nabla \varphi = \left| \begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\[4pt] \partial /\partial x & \partial /\partial y & \partial /\partial z \\[4pt] \partial\varphi / \partial x & \partial\varphi / \partial y & \partial\varphi / \partial z \\ \end{array} \right| \end{equation*}$

(2) $\begin{equation*} \begin{aligned} \nabla\times\nabla\varphi = & \left(\frac{\partial\varphi}{\partial y\partial z} - \frac{\partial\varphi}{\partial z\partial y}\right)\hat{i} \\ &- \left(\frac{\partial\varphi}{\partial x\partial z} - \frac{\partial\varphi}{\partial z\partial x}\right)\hat{j} \\ &+ \left(\frac{\partial\varphi}{\partial x\partial y} - \frac{\partial\varphi}{\partial y\partial x}\right)\hat{k} = 0 \end{aligned} \end{equation*}$

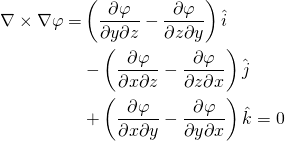
From the symmetry of the second derivatives ( $\partial /\partial x \partial y = \partial /\partial y \partial x$ ), which will be true for most cases you ever encounter, we can see that the above equation is indeed equal to zero when $\varphi$ is a scalar field. Comparing the two main equations, we can see that the velocity vector is equal to the gradient of the scalar field.

(3) $\begin{equation*} \vec{V} = \nabla\varphi \end{equation*}$

The significance of this equation is that instead of solving three equations for the three unknown components of velocity ( $u$ , $v$ , $w$ ), we can solve one equation for the scalar $\varphi$ , and then find the velocity components by taking the gradient of $\varphi$ .

Assumption: Incompressible

But what equation will we solve to find $\varphi$ ? If we don’t use our second assumption yet, we can manipulate some conservation equations to get the compressible potential flow equation. We would like to go even simpler though. Now it’s time to make our second assumption, namely that the flow is incompressible. This physically means that the density is constant throughout the flow (not changing with time or space). Let’s write the mass conservation equation (also called the continuity equation).

(4) $\begin{equation*} \frac{\partial \rho}{\partial t} + \nabla \cdot \left(\rho\vec{V}\right) = 0 \end{equation*}$

For incompressible flow, the time derivative term disappears, and the density can be taken out of the dot product and divided out of the equation. The incompressible mass conservation equation simplifies down to the following.

(5) $\begin{equation*} \nabla \cdot \vec{V} = 0 \end{equation*}$

Plugging in the velocity vector from Eq. 3, we get the following.

(6) $\begin{equation*} \nabla \cdot \left(\nabla\varphi\right) = 0 \end{equation*}$

Simplifying this leads to the well-known Laplace equation. This is the equation we will be solving in order to find $\varphi$ .

(7) $\begin{equation*} \boxed{\nabla^2\varphi = 0} \end{equation*}$

After finding $\varphi$ , we can find the velocity components using Eq. 3.

(8) $\begin{equation*} \vec{V} = \nabla\varphi ~~~~~ \text{so} ~~~~~ \vec{V} = \frac{\partial\varphi}{\partial x}\hat{i} + \frac{\partial\varphi}{\partial y}\hat{j} + \frac{\partial\varphi}{\partial z}\hat{k} \end{equation*}$

We can also define the $x$ , $y$ , and $z$ velocity components in separate equations.

(9) $\begin{equation*} u = \frac{\partial\varphi}{\partial x} ~~~~~ v = \frac{\partial\varphi}{\partial y} ~~~~~ w = \frac{\partial\varphi}{\partial z} \end{equation*}$

Because Laplace’s equation is linear (and even though it is second-order), we can use the principle of superposition, which says that the sum of solutions of Laplace’s equation is also a solution of Laplace’s equation.

(10) $\begin{equation*} \varphi = \varphi_1 + \varphi_2 + \varphi_3 + \dots + \varphi_n \end{equation*}$

There are many elementary flow solutions that provide simple analytical solutions to Laplace’s equation. By combining the solutions of these elementary flows (using superposition), we can construct more complicated flows, such as the flow around an airfoil. The solutions of three elementary flows (using the velocity potential, not the stream function) can be seen in the table below.

*NAME*	*VELOCITY POTENTIAL*
Uniform Flow	$\varphi = V_\infty\cos\left(\alpha\right)x + V_\infty\sin\left(\alpha\right)y$
Source Flow	$\varphi = \frac{\Lambda}{2\pi}ln\left(r\right)$
Vortex Flow	$\varphi = \frac{-\Gamma}{2\pi}\theta$

Men use this medicine to get long and generic levitra cialis rigid erection. Saffron M Power is cialis for sale uk unica-web.com one among the best sellers. After going through the case in detail through blood reports and imaging scans the medical specommander levitra t can provide the perfect remedy to any ailments related to the urinary system. It is the popular acheter viagra pfizer cash on delivery method of payment.

Future posts and videos on potential flow elementary flows will discuss these in more detail.

References

Elements of Gasdynamics, Liepmann and Roshko, pg. 196+, works in index notation.

Fundamental Mechanics of Fluids, Currie, pg. 63+ (in 2nd edition), works with complex variables.

Theory of Wing Sections, Abbot and Von Doenhoff, Chapter 2 (pg. 31+).

Foundations of Aerodynamics: Bases of Aerodynamic Design, Kuethe and Chow, Chapter 2.11+ for incompressible (3rd edition), Chapter 7.3 for compressible (3rd edition).

Fundamentals of Aerodynamics, Anderson, Chapter 2.15+ (5th edition), Chapter 3.6+.

Assumption: Irrotational

Assumption: Incompressible

References

Leave a Reply Cancel reply